Dijkstra 算法

Dijkstra Algorithm

迪杰斯特拉（按照读音，应该读作戴克斯特拉）算法是用于求解单源最短路径的经典算法。

单源最短路径问题

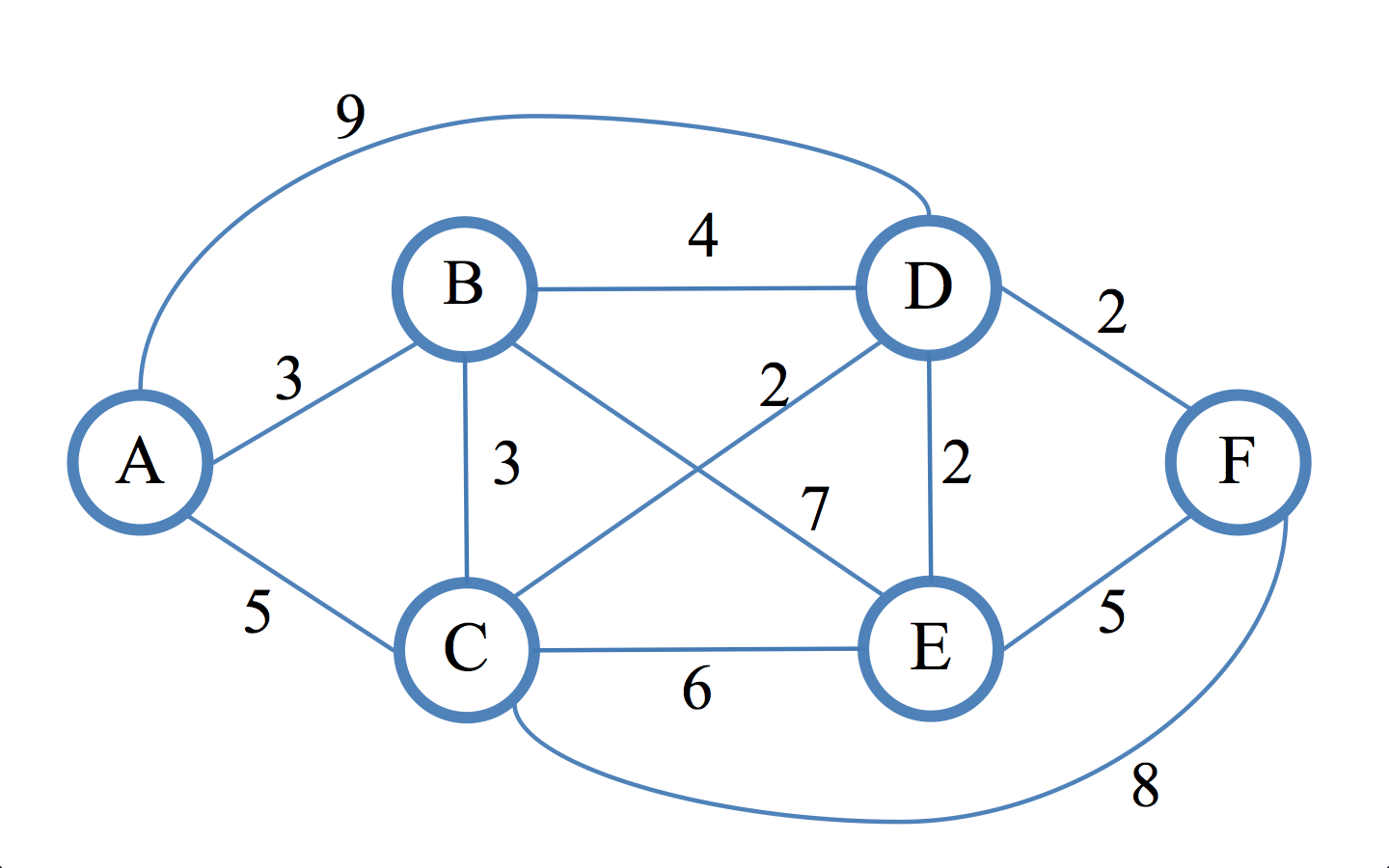
在一个带权的图中，从某个特定的起始点（源）出发，计算到某个终点的最短路径，这种问题被称为单源最短路径问题。

Dijkstra算法思路

Dijkstra算法基于贪心思想，具体思路为：维护一个“已确定”的顶点集合和“未确定”的顶点集合，用“已确定”的顶点对“未确定”集合中的顶点不断地更新，并把“未确定”的顶点一个个加入“已确定”集合，最终确定下所有的顶点的最短路径。

每一轮，在“未确定”的集合中选出距离源点路径最短的顶点A，把这个顶点确定下来加入到”已确定“顶点集合。原因是：这个点A的最短路径想要更新，必须要找到一个点B，它的路径更短，这样加上这个点到当前节点的边B->A，才有机会比当前A得最短路径更短。但是所有满足这种条件的A都已经被“确定“了，不能再用了，因为我们已经用过了。剩下“未确定”的点，最短都一定大于等于当前A得最短距离，那么肯定对A是帮不上忙的。

现在A被“确定”了，“已确定”点集又填新成员，就可以试试再用这个新成员来“帮助”未确定的顶点。具体而言，即遍历A直接指向的顶点，尝试用A得最短路径加上A到它们的距离，来更新它们的最短路径。如果dist(A)+edge<A, B>小于dist(B)，B的最短路径就可以变成先从源点走A的最短路径到A，再从A到B。这被称为一次“松弛”操作。这个词很有意思，想象两个节点由一根绳子连接，现在来了一根更短的绳子，使劲把它们连在一起，原来的绳子就松弛了。

如此循环这个操作，直到所有节点都被确定，整个图所有节点的单源最短路径就确定了。

条件

刚才提到，为什么不用剩下的节点来更新A，是因为剩下的节点路径更长，对A帮不上忙。而这是基于一个前提，就是不存在负边权。如果存在负边权，这个更新逻辑就不成立了，整个Dijkstra算法就失效了。

优化

在寻找“未确定”集合中的最小值时，如果每次都一个一个比较，太慢了。我们可以用小根堆（优先队列）来优化这个过程

例题

LeetCode 743 网络延迟时间

题目链接

题目描述：

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        graph = dict()
        hp = []
        final_vertices = set()
        # build graph
        for time in times:
            source, target, weight = time
            if source not in graph:
                graph[source] = []
            graph[source].append([target, weight])
        
        heapq.heappush(hp, (0, k))
        
        max_dist = 0
        # Dijkstra Algorithm
        while len(hp):
            dist, top = heapq.heappop(hp)
            if top not in final_vertices:
              	# 这一步判断很重要，因为我们的优先队列中同一个顶点可能出现多次，但是一定只有最先遇到的才是最短的路径，剩下的直接丢掉就好
                max_dist = dist
                if top in graph:
                    for target, weight in graph[top]:
                      	# 对每个节点尝试执行“松弛”操作
                        if target not in final_vertices:
                            heapq.heappush(hp, (dist + weight, target))
                final_vertices.add(top)

        if len(final_vertices) == n:
            return max_dist
        
        return -1